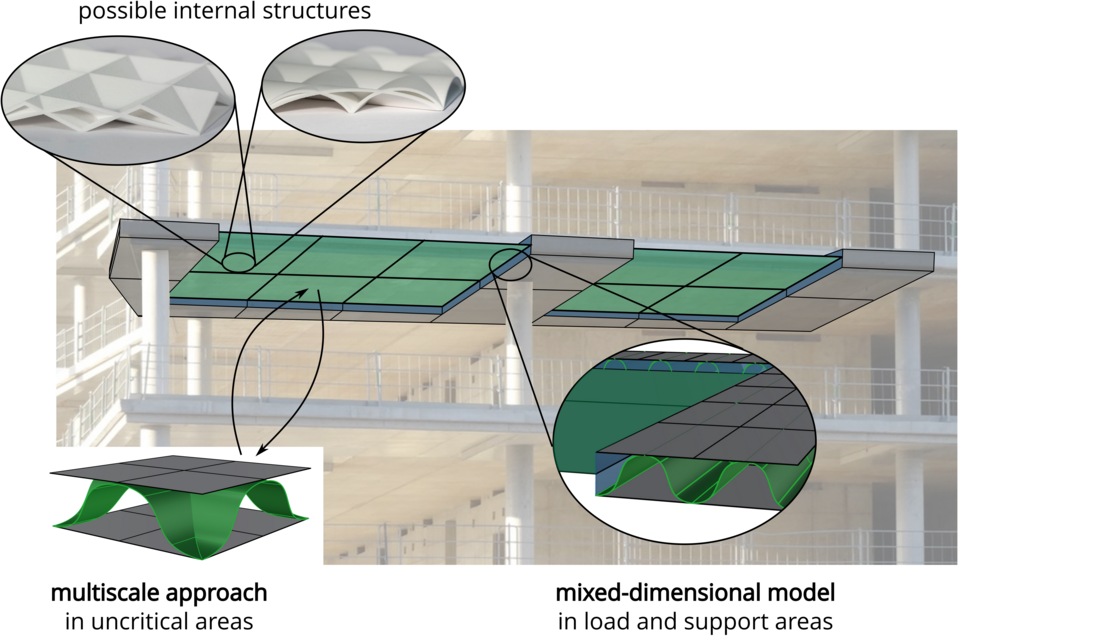
In this project, we analyze the load-bearing behavior of structural components with a resolved internal structure using numerical methods. Two complementary approaches are being pursued: the development of a multiscale method and of a mixed-dimensional substructure method. A common feature of both methods is that they are based on shell elements, which is advantageous due to the numerical efficiency of these elements.

First, we develop a multiscale method, which separates the structural component into two scales. On the coarse scale the geometry of the structural component is represented by shell elements, while on a finer scale the resolved internal structure is captured by a representative volume element (RVE). The developed multiscale method follows a coupled approach (FE² method) to account for geometric and physical nonlinearities. Second, we use a mixed-dimensional substructure method, complementing the developed multiscale method in the support and load areas of the structural component. In these areas, the structure is modeled in three dimensions to ensure an adequate analysis of the load-bearing

behavior. However, most of the structure is still modeled with two-dimensional shell elements. To correctly link the different kinematics between three-dimensional model and shell elements we will develop a transition element that avoids spurious stresses.

Since the multiscale method enables the analysis of large-span structural components and the mixed-dimensional method allows the detailed analysis of critical regions, these methods can be used in combination to accurately and efficiently describe carbon-reinforced resolved concrete shell structures.

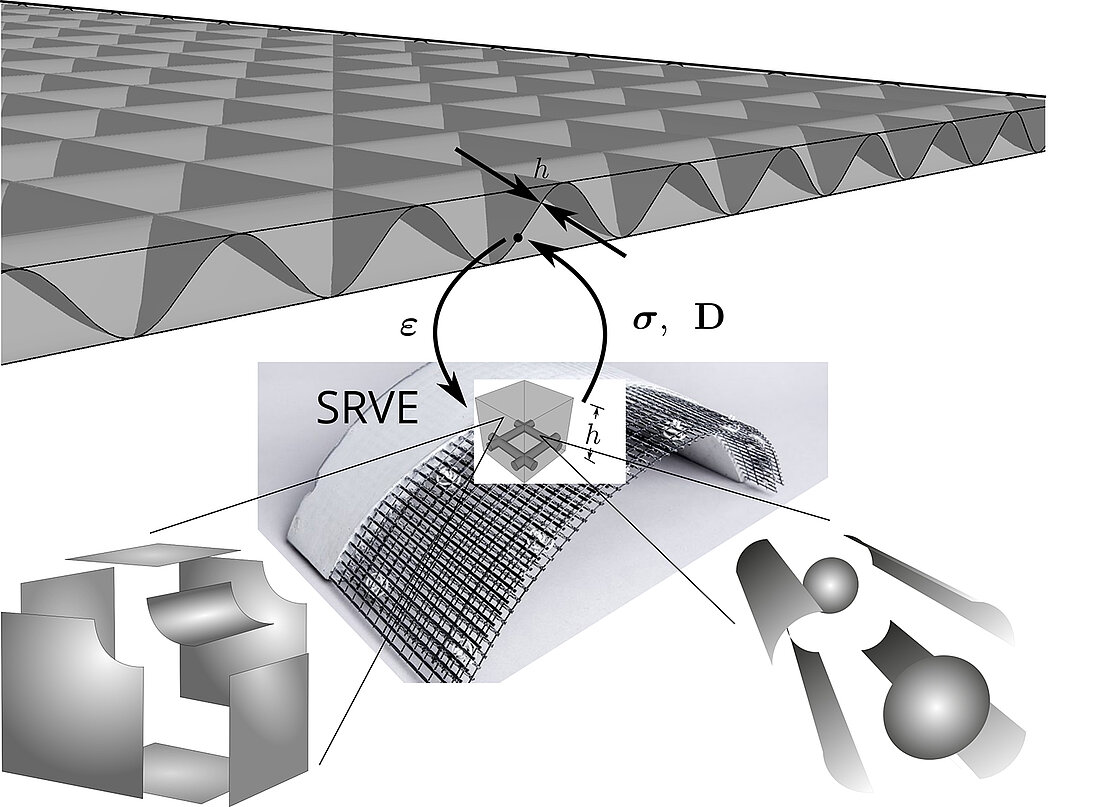
This project focusses on the in-silico design of thin, curved carbon-fiber reinforced concrete shell structures using the finite element method (FEM). With respect to efficiency, especially shell elements are suitable. In the scope of this project a numerical multi-scale model is to be developed. By homogenization of a representative volume element, which is able to incorporate shell kinematics (SRVE), the modelling of the carbon-fiber reinforcement and the use of 3D material laws is possible. To allow for geometrical and physical nonlinearities a coupled multi-scale method is used for calculation (FE²-method).

To reduce the numerical cost a new formulation based on the scaled-boundary finite element method (SBFEM) is used. The geometry is described using NURBS-based shape functions. This results in an isogeometric analysis for scaled boundaries (SBIGA).

Imaging techniques are used to create and validate the model. Using level-set or marching-cubes algorithms the surface description of the carbon-fiber rovings and the concrete are extracted from CT data. Using the above-mentioned element formulation, a numerical model of the structure is obtained.

Associated with the project C03 is the supplementary project C03*: Computational Homogenization and Multi-Scale Modelling Employing an Image-Based Approach for the Structural Analysis of Shells.