Multiscale and mixed-dimensional substructure modeling of carbon-reinforced resolved concrete shell structures | Funding Period 2
In this project, we analyze the load-bearing behavior of structural components with a resolved internal structure using numerical methods. Two complementary approaches are being pursued: the development of a multiscale method and of a mixed-dimensional substructure method. A common feature of both methods is that they are based on shell elements, which is advantageous due to the numerical efficiency of these elements.
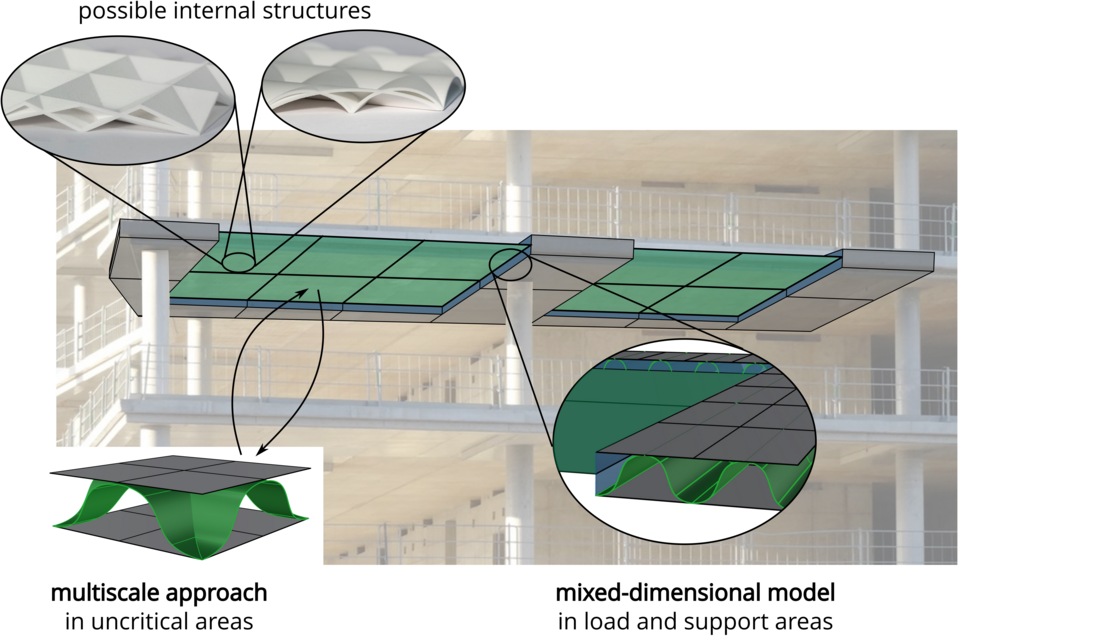
First, we develop a multiscale method, which separates the structural component into two scales. On the coarse scale the geometry of the structural component is represented by shell elements, while on a finer scale the resolved internal structure is captured by a representative volume element (RVE). The developed multiscale method follows a coupled approach (FE2 method) to account for geometric and physical nonlinearities. Second, we use a mixed-dimensional substructure method, complementing the developed multiscale method in the support and load areas of the structural component. In these areas, the structure is modeled in three dimensions to ensure an adequate analysis of the load-bearing
behavior. However, most of the structure is still modeled with two-dimensional shell elements. To correctly link the different kinematics between three-dimensional model and shell elements we will develop a transition element that avoids spurious stresses.
Since the multiscale method enables the analysis of large-span structural components and the mixed-dimensional method allows the detailed analysis of critical regions, these methods can be used in combination to accurately and efficiently describe carbon-reinforced resolved concrete shell structures.
Scientists
![Prof. Dr.-Ing. habil. Sven Klinkel [Translate to English:] Sven Klinkel](/fileadmin/_processed_/c/f/csm_A-Klinkel_Quadratisch_bd2b0ef37c.jpg)
D-52074 Aachen (Germany)

52074 Aachen
![M.Sc. Marja-Lisa Herrmann [Translate to English:] Protraitbild](/fileadmin/_processed_/3/9/csm_Hermann_quadratisch_4edf4194d2.jpg)
52074 Aachen
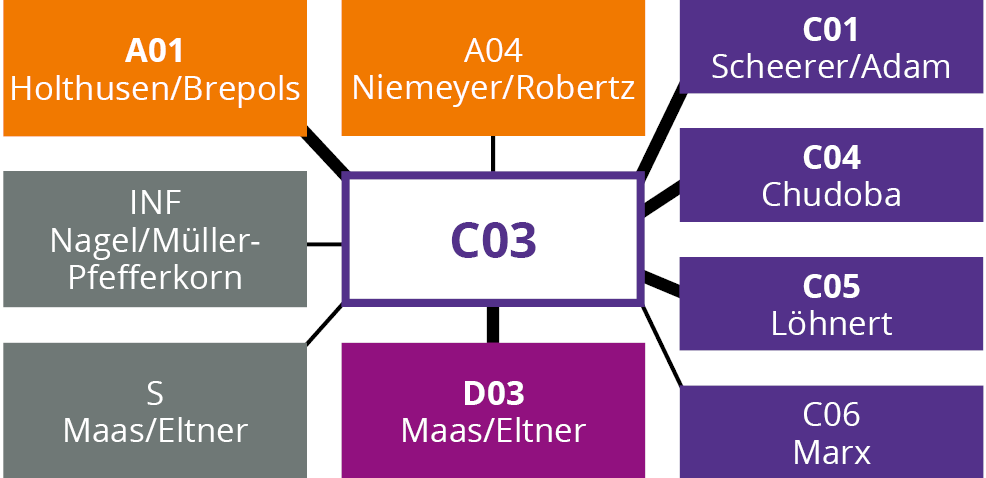
Kooperationen
Computational Homogenization and Multi-Scale Modelling Employing an Image-Based Approach for the Structural Analysis of Shells | Funding Period 1
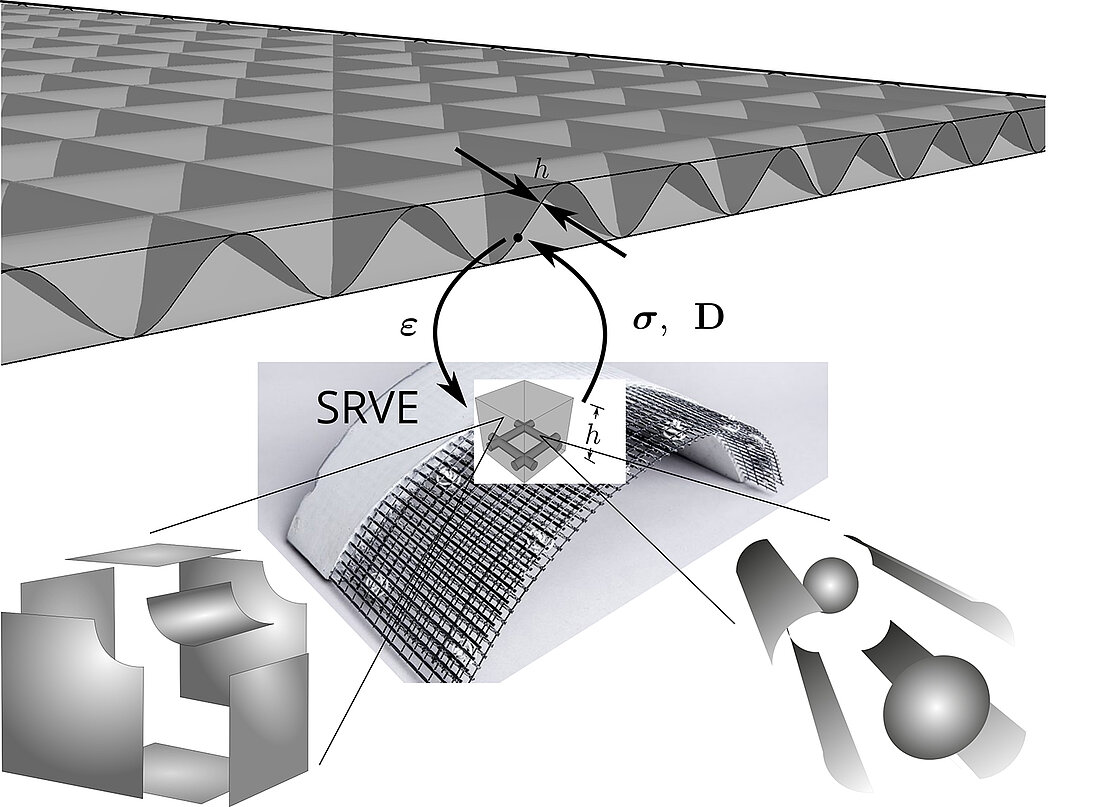
This project focusses on the in-silico design of thin, curved carbon-fiber reinforced concrete shell structures using the finite element method (FEM). With respect to efficiency, especially shell elements are suitable. In the scope of this project a numerical multi-scale model is to be developed. By homogenization of a representative volume element, which is able to incorporate shell kinematics (SRVE), the modelling of the carbon-fiber reinforcement and the use of 3D material laws is possible. To allow for geometrical and physical nonlinearities a coupled multi-scale method is used for calculation (FE2-method).
To reduce the numerical cost a new formulation based on the scaled-boundary finite element method (SBFEM) is used. The geometry is described using NURBS-based shape functions. This results in an isogeometric analysis for scaled boundaries (SBIGA).
Imaging techniques are used to create and validate the model. Using level-set or marching-cubes algorithms the surface description of the carbon-fiber rovings and the concrete are extracted from CT data. Using the above-mentioned element formulation, a numerical model of the structure is obtained.
Associated with the project C03 is the supplementary project C03*: Computational Homogenization and Multi-Scale Modelling Employing an Image-Based Approach for the Structural Analysis of Shells.

Publikationen | Publications
Chasapi, M.; Mester, L.; Simeon, B.; Klinkel, S. (2022) Isogeometric analysis of 3D solids in boundary representation for problems in nonlinear solid mechanics and structural dynamics in: Int J Numer Methods Eng 123, issue 5, p. 1228–1252– DOI: 10.1002/nme.6893
Curosu, V.; Kikis, G.; Krüger, C.; Liebold, F.; Macek, D.; Mester, L.; Platen, J.; Ritzert, S.; Stüttgen, S.; Kaliske, M.; Klinkel, S.; Loehnert, S.; Maas, H.-G.; Reese, S.; Robertz, D. (2023) Ansätze für numerische Methoden zur Inspiration, Analyse und Bewertung neuartiger Carbonbetonstrukturen in: Bauingenieur 98, issue 11, p. 368–377 – DOI: 10.37544/0005-6650-2023-11-56
Klarmann, S.; Kikis, G.; Klinkel, S.; Chudoba, R. (2023) Isogeometric cohesive zone modeling of interfaces in reinforced concrete structures in: Proc. Appl. Math. Mech. – DOI: 10.1002/pamm.202300160
Mester, L.; Klarmann, S.; Klinkel, S. (2021) A homogenisation approach for shell structures using scaled boundary isogeometric analysis on RVE-level in: Proc. Appl. Math. Mech. 21, issue 1 – Special Issue: 92nd Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM), 15.–19.03.2021 in Kassel, e202100157, 2 p. – DOI: 10.1002/pamm.202100157
Mester, L.; Klarmann, S.; Klinkel, S. (2023) Homogenisation for macroscopic shell structures with application to textile‐reinforced mesostructures in: Proc. Appl. Math. Mech. 22, issue 1 – Special Issue: 92nd Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM), e202200137 – DOI: 10.1002/pamm.202200137
Mester, L.; Klarmann, S.; Klinkel, S. (2023) Homogenization assumptions for the two-scale analysis of first-order shear deformable shells in: Comput Mech – DOI: 10.1007/s00466-023-02390-z
Mester, L.; Klempt, V.; Wagner, F.; Scheerer, S.; Klarmann, S.; Vakaliuk, I.; Curbach, M.; Maas, H.-G.; Löhnert, S.; Klinkel, S. (2023) A Comparison of Multiscale Methods for the Modelling of Carbon-Reinforced Concrete Structures in: Ilki, A.; Çavunt, D.; Çavunt, Y. S. [eds.] Building for the Future: Durable, Sustainable, Resilient – Proc. of fib Symposium 2023, 05.–07.06.2023 in Istanbul (Turkey), publ. in: Lecture Notes in Civil Engineering 350, Cham: Springer, p. 1418–1427 – DOI: 10.1007/978-3-031-32511-3_145
Mester, L.; Wagner, F.; Liebold, F.; Klarmann, S.; Maas, H.-G.; Klinkel, S. (2022) Image-based modelling of carbon-fibre reinforced concrete shell structures in: Stokkeland, S.; Braarud, H. C. [eds.] Concrete Innovation for Sustainability – Proc. for the 6th fib International Congress 2022, 12.–16.06.2022 in Oslo (Norway), Oslo: Novus Press, p. 1631–1640.
Wagner, F.; Mester, L.; Klinkel, S.; Maas, H.-G. (2023) Analysis of Thin Carbon Reinforced Concrete Structures through Microtomography and Machine Learning in: Buildings 13, issue 9, 2399 – DOI: 10.3390/buildings13092399
Dissertation | Doctoral thesis
Leonie Mester:Computational Homogenisation and Multiscale Modelling Employing an Image-based Approach for the Structural Analysis of Shells [Doktorarbeit | doctoral thesis]. RWTH Aachen, Datum der mündlichen Prüfung | Date of oral examination: 01.03.2024, publiziert | published: 2024, https://publications.rwth-aachen.de/record/992740/files/992740.pdf | DOI: 10.18154/RWTH-2024-08387
Studentische Arbeiten | Student's works
Krusche, J. (2023) Bildgebende Verfahren zur Modellierung von Carbonbeton [Bachelorarbeit | Bachelor’s thesis]
Sevindik, J. (2023) Entwicklung und Implementierung eines Pre-Prozessors zur Verarbeitung von NURBS-Oberflächen im Rahmen der Scaled Boundary Isogeometric Analysis [Bachelorarbeit | Bachelor’s thesis]
Lenze, C. (2023) The Influence of the Scaling Center Position on the Uniqueness of Solutions in the Scaled Boundary Finite Element Method [Bachelorarbeit | Bachelor’s thesis]
Elisová, A. (2022) Comparison of Different Numerical Models for Concrete and their Implementation [Masterarbeit | Master’s thesis] mit | with C03*
Spahn, F. (2022) Development and Implementation of a Scaled Boundary Formulation for Slender Beam-like Structures for Anisotropic Fibre-Matrix Materials [Masterarbeit | Master’s thesis]
Pierick, B. (2021) Computation of the scaling center for arbitrarily shaped polygons for the application in the Scaled Boundary Finite Element Method using Deep Convolutional Neural Networks [Bachelorarbeit | Bachelor’s thesis]




