Algebraic investigation of static properties of simplicial surfaces

Three-dimensional triangulated surfaces, so-called simplicial surfaces, are a mathematical source of inspiration for folded carbon-reinforced concrete components. The geometrically exact description of these components is difficult, as it requires solving large polynomial systems of equations. Furthermore, during the step-by-step construction of such surfaces, so-called non-rigid configurations can occur in which the surface exhibits non-trivial motions of the vertices without altering edge lengths. It is of interest for the TRR 280 to understand these motions, as the existence of unintended, flexible motions can compromise the integrity of a carbon-reinforced concrete structure. Conversely, such motions could be utilized in a construction process as degrees of freedom or simplify the transport of carbon-reinforced concrete components.

Therefore, this seed fund project aims to explore numerical and algebraic approaches for describing simplicial surfaces algebraically and analyzing their rigidity.

Results:

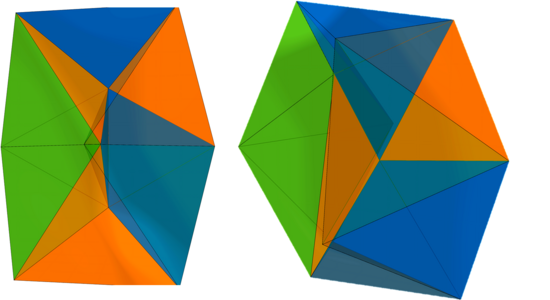
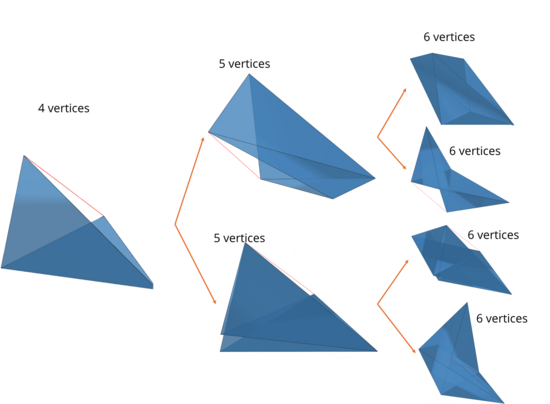
• Development and implementation of an algorithm that calculates all 3-dimensional realizations for a given combinatorial simplicial surface (only vertex-edge-face adjacency is given) and specified edge lengths.
  By adding new edges, the surface is subdivided into tetrahedra. The surface is then realized sequentially. The runtime of the algorithm is exponential in the number of vertices. Future work will explore reducing this complexity, possibly through a priori knowledge of the resulting geometry.

• Implementation of a particle simulation for rigidity analysis of a simplicial surface.
  Vertices of a given simplicial surface are treated as physical particles distance-constrained by existing edges. Applying physical forces to these particles the system's behavior is simulated.

• Numerical methods such as gradient descent, Gauss-Newton, or homotopy continuation can be used to find solutions for the resulting systems of equations but are not suitable for classifying all solutions. Further work will investigate how numerical solutions can be used to improve the first algorithm.

• A related field to rigidity analysis is the analysis of the topological locking property (see publication in cooperation with other TRR researchers).