Algebraische Untersuchung statischer Eigenschaften von Flächen
Dreidimensionale triangulierte Flächen, sogenannte simpliziale Flächen, sind eine mathematische Inspirationsquelle für gefaltete Carbonbetonteile. Die geometrisch exakte Beschreibung dieser Bauteile ist sehr schwierig, da dafür große polynomielle Gleichungssysteme gelöst werden müssen. Weiter kann es während der schrittweisen Konstruktion solcher Flächen zu sogenannten nicht-starren Konfigurationen kommen, bei denen die Fläche nicht-trivial bewegt werden kann, ohne dass sich die Kantenlängen verändern. Es ist von Interesse für den Transregio 280, diese Bewegungen besser zu verstehen, da eine ungewollte, flexible Bewegung die Integrität einer Konstruktion aus Carbonbeton gefährden kann. Andererseits könnten solche Bewegungen bei der Errichtung von Strukturen als Freiheitsgrade ausgenutzt werden oder den Transport von Carbonbetonbauteilen vereinfachen.
Deshalb sollen in diesem Seedfundprojekt numerische und algebraische Ansätze erarbeitet werden, um simpliziale Flächen algebraisch exakt zu beschreiben und ihre Starrheit zu analysieren.
Ergebnisse:
- Entwicklung und Implementierung eines Algorithmus, welcher zu einer gegebenen kombinatorischen simplizialen Fläche (nur Information über Vertex-Kanten-Flächen-Verbindungen) und vorgegebenen Kantenlängen alle 3-dimensionalen Realisationen berechnet.
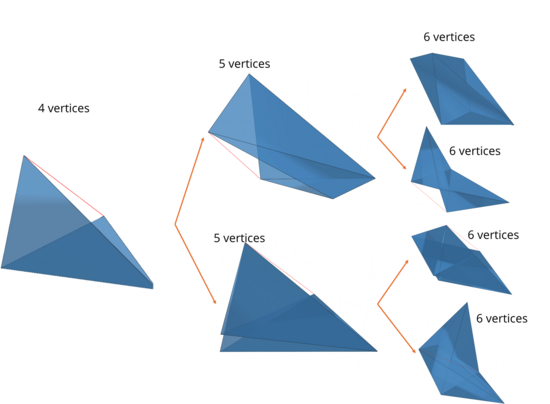
Durch Hinzufügen neuer Kanten wird die Fläche in Tetraeder unterteilt. Anschließend wird die Fläche Tetraeder für Tetraeder realisiert. Die Laufzeit des Algorithmus ist exponentiell in der Anzahl der Vertizes. In weiterer Arbeit soll deshalb untersucht werden, wie die Komplexität des Ansatzes verringert werden kann, beispielsweise durch a priori Kenntnisse über die entstehende Geometrie. Implementierung einer Partikelsimulation für die Starrheitsanalyse einer simplizialen Fläche.
Für eine gegebene simpliziale Fläche werden ihre Vertizes als physikalische Partikel angesehen, welche durch die vorhandenen Kanten Abstandsbedingungen ausgesetzt sind. Es werden Kräfte auf die Partikel angewandt und das Verhalten des Systems simuliert.Numerische Methoden wie Gradient Descent, Gauß-Newton oder Homotopy Continuation können verwendet werden, um Lösungen für die entstehenden Gleichungssysteme zu finden, eignen sich aber nicht dafür, alle Lösungen zu klassifizieren. In weiterer Arbeit soll untersucht werden, wie numerische Lösungen verwendet werden können, um den ersten Algorithmus zu verbessern.
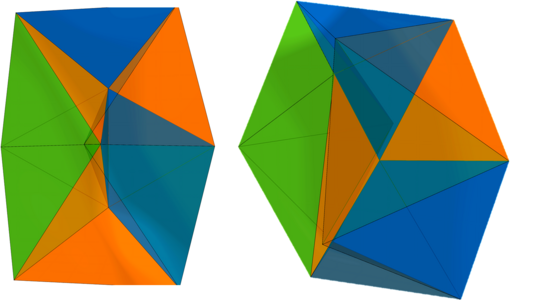
Ein verwandtes Gebiet zur Starrheitsanalyse ist die Analyse der topologischen Verriegelungseigenschaft (s. Veröffentlichung in Kooperation mit anderen Forscher*innen des TRR 280).
Veröffentlichungen | Publications
Stüttgen, S.; Akpanya, R.; Beckmann, B.; Chudoba, R.; Robertz, D.; Niemeyer, A. C. (2023)Modular Construction of Topological Interlocking Blocks—An Algebraic Approach for Resource-Efficient Carbon-Reinforced Concrete Structures in Buildings 13, issue 10, 2565 – DOI: https://doi.org/10.3390/buildings13102565
Team

52062 Aachen

52062 Aachen




