Verbundverhalten zwischen aufgelösten inneren Schalenstrukturen

Bei Stahlbetonkonstruktionen ist die korrekte Erfassung des Verbundes zwischen Beton und Bewehrung eine anspruchsvolle Aufgabe, da hier verschiedene Mechanismen gleichzeitig wirken. Die genaue Beschreibung der Geometrie der Bewehrung ist jedoch bei der Verwendung von Lagrange-Ansatzfunktionen nicht möglich und kann die Modellierung dieser Interaktion zusätzlich beeinflussen. Die isogeometrische Analyse ermöglicht die exakte Darstellung komplexer Geometrien und kann so die Beschreibung  des Verbundverhaltens verbessern. Sowohl die Betonmatrix als auch die Bewehrung werden mittels ihrer Randflächen in Verbindung mit NURBS und B-Splines (SBIGA) dargestellt, was der Modellierungstechnik in CAD-Tools entspricht. Dies ermöglicht eine unkomplizierte Verwendung des Entwurfsmodells im Analyseprozess. Die Interaktionsmechanismen zwischen der Bewehrung und dem Beton werden mit Hilfe einer dickenfreien Grenzfläche in Kombination mit einem thermodynamisch konsistenten Kohäsionszonenmodell modelliert, welches die Dekohäsions-, Druck- und Gleiteffekte erfasst. Es beinhaltet eine gekoppelte Schädigungs-Plastizitäts-Dissipation für die normale und tangentiale Richtung.

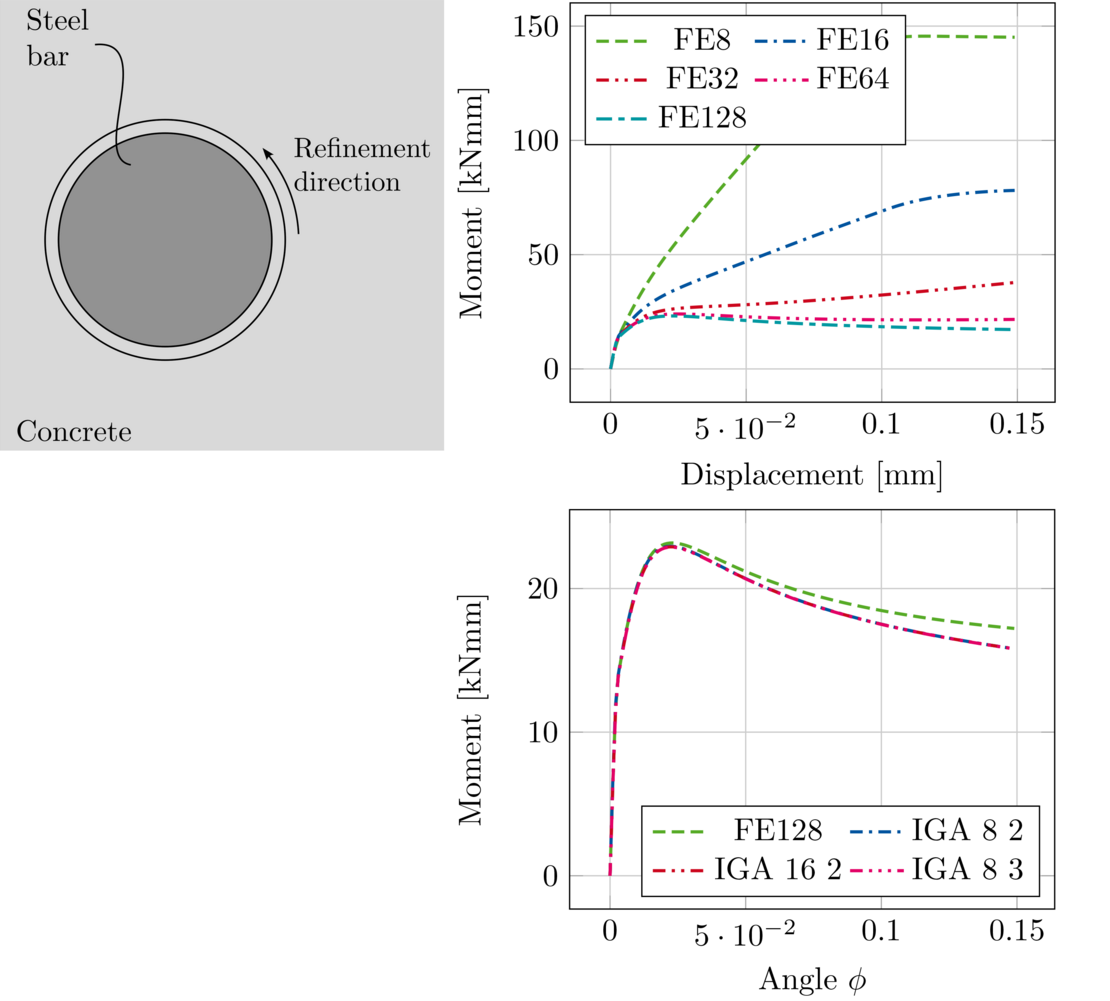
Das Modell wurde anhand von Versuchsergebnissen verifiziert. Weiterhin wurde ein Vergleich mit der Standard-Finite-Elemente-Methode durchgeführt, um die Vorteile der Anwendung der isogeometrischen Analyse für die genaue Darstellung der Bewehrung zu untersuchen.